Hi, everyone!
As some people know, I have got interest in theory of games. Well, this post is going to be dedicated to this subject.
My aim here is to introduce some aspects of game theory and the prisoner’s dilemma, presupposing no previous knowledge.
First of all, it would be nice to explain a little bit about a model of game.
For simplicity, the components of a game are: Players, Actions, Payoffs.
Players
USSR and USA played a game known as Arms Race in the Cold War
In theory of games we must have a minimum of 2 players. If you are dealing with just one player, you have to try another one: decision theory.
To identify who are the players, a good question is: “Does the action of one player affect the other?” If the answer is ‘yes’, there is a good chance that he/she is actually a player.
If you want a better explanation why a minimum of 2 players take a look at the Robinson Crusoe’s citation in the foundation book of theory of games from von Neumann (R. 1)
Actions
The rules of chess give the set of actions for each player
If we don’t have a set of actions, we don’t have any strategy to follow, so we don’t have a game. Actions are an essential part of a game. There must have a set of actions for each player.
Payoffs
Payoffs roughly speaking are functions that map what players get given a strategy profile. It is another essential piece of the puzzle. Payoffs may represent the player’s preferences (utility function) too.
Now, let’s see the prisoner’s dilemma situation.
The game
“Two men suspected of commiting a crime together are arrested and placed in separate cells by the police. Each suspect may either confess or remain silent, and each one knows the possible consequences of his action. These are: (1) If one suspect confesses and his partner does not, the one who confessed turns state’s evidence and goes free and the other one goes to jail for twenty years. (2) If both suspects confess, they both go to jail for five years. (3) If both suspects remain silent, they both go to jail for a year for carrying concealed weapons – a lesser charge.” ( R.2 ) Communication between the suspects is not allowed and they have to decide simultaneously.
Well, this is the story.
Let’s try to model the situation:
Players:
{Suspect I, Suspect II}
Actions:
Suspect I: {confess, don’t confess}
Suspect II: {confess, don’t confess}
Payoffs:
If we define a strategy profile as a tuple where the first coordinate represents the action for Suspect I and the second for the Suspect II, we have the following possibilities for outcomes:
(suspect I action, suspect II action) -> suspect I payoff
(confess, confess) -> 5 years
(confess, don’t confess) -> 0 years
(don’t confess, confess) -> 20 years
(don’t confess, don’t confess) -> 1 year
As you can see, the payoff of the suspect I depends on the suspect II action. There is a mathematical function that could be better formalized, but it’s ok like that for our purpose here.
We did not name the suspects, so the same payoff function is symmetric for the other player.
It’s common in game theory books use a table to organize the information:
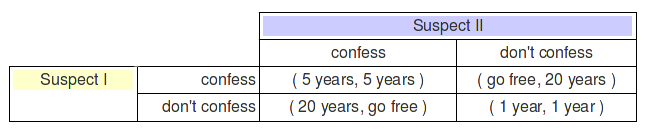
It’s done! We modeled the prisoner’s dilemma from scratch!
Solving the game
Now, what do you think that it’s going to happen? What would each suspect do? What would you do?
Well, there are a lot of explanations and considerations in this game.
To begin our analysis, let’s simplify the model:
Let’s analyze the table.
If Suspect II does confess, Suspect I take 5 years choosing confess. If Suspect I chooses DC he/she gets 20 years, therefore is better to confess.
If Suspect II don’t confess, Suspect I go free choosing confess. If Suspect I chooses DC he/she gets 1 year, therefore is better to confess.
Thus, choosing to confess is the best response no matter what Suspect II does.
The jargon used in the literature is C ‘strictly dominates’ DC.
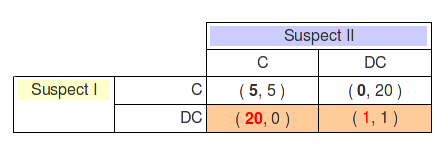Action C strictly dominates DC for Suspect I
So, reasoning the same way for the other player:
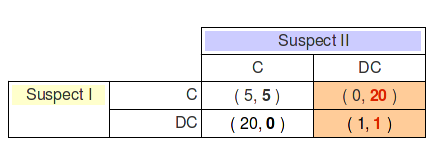Action C strictly dominates DC for Suspect II
Rational Players:
There is one hypothesis in theory of games that must be true in order to make it useful. The hypothesis is that the players are rational. What means by being rational is something that I’ll let for another post. But essentially it means that the players have consistent preferences (transitive relation). It doesn’t follow that being rational implies that there is only one preference order, that is, the theory doesn’t tell what players want. Only the players can tell what they want (their goals and preferences).
In the prisoner’s dilemma, the players prefer to stay away from the jail. It would be ok if they liked to be on jail, but the game would be other, because once you change a component of the game, you changed the game.
The prisoners want to minimize their time in the jail. Then, backing to our problem, if the 2 suspects are rationals they wouldn’t play a dominated strategy. So, the game ends with an equilibrium, the (Confess, Confess) strategy profile:
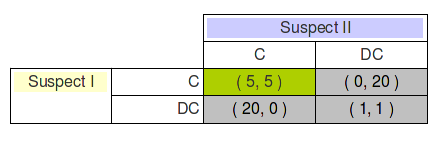(C, C) is the Nash Equilibrium for the game
The paradox
The paradox that someone may claim is that both would do better if both collaborated, choosing (Don’t confess, Don’t confess). Nevertheless, no one is secured that the other will collaborate. Even if they both could communicate, in the last move one could deviate. So, it’s better to choose confess.
Well, that’s all for now.
I’d like to pardon all of you that master game theory since my language in this post was really imprecise, without rigor and maybe unpolite.
References:
R. 1 -> von Neumann, John; Morgenstern, Oskar (1944), Theory of games and economic behavior, Princeton University Press
R. 2 -> Davis, Morton. Game Theory – a nontechnical introduction
Hi, everyone!
When you switch it on for the first time, you get a blue light.
F r a c t a l R o a d 